POLÍGONOS
POLIGONOS
Definicion:
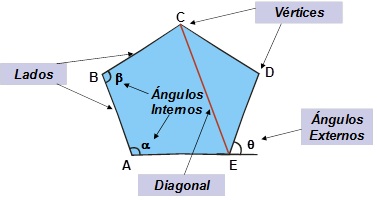
Polígonos es la porción de plano limitada por una línea poligonal cerrada. Elementos: 1) Lados: Son los segmentos rectilíneos que lo limitan: AB, BC, CD, DE, etc. 2) Vértices: Son las intersecciones de dos lados consecutivos, los vértices son: A, B, C, D, etc. 3) Ángulos interiores: Son los ángulos formados por dos lados consecutivos. 4) Ángulos exteriores: Son los ángulos formados en un vértice por un lado y la prolongación del lado consecutivo. 5) Diagonales: Son líneas rectas que unen dos vértices no consecutivos. AD, AC, BE.
Clasificacion:
Se clasifican: Por el número de sus lados y por la forma de su contorno.
A.-Por el número de sus lados:
Nº de Lados | Nombre | Nº de Lados | Nombre |
3 | Triángulo | 9 | Eneágono o nonágono |
4 | Cuadrilátero | 10 | Decágono |
5 | Pentágono | 11 | Endecágono |
6 | Exágono o hexágono | 12 | Dodecágono |
7 | Eptágono o heptágono | 15 | Pentadecágono |
8 | Octágono u octógono | 20 | Icoságono |
B.-Por la forma de su contorno:
- Convexos: Son aquellos polígonos, en los que al atravesarlos una recta lo cortan en un máximo de dos puntos.
- Cóncavos: Son aquellos polígonos, en los que una recta al atravesarlos pueden cortar en más de dos puntos.
- Equiláteros: Son los polígonos que tienen todos sus lados iguales.
- Equiángulos: Son los polígonos que tienen sus ángulos iguales.
- Regulares: Son los polígonos que tienen sus ángulos y sus lados iguales entre sí.
-Irregulares: Son los polígonos que tienen sus ángulos y lados desiguales.
Propiedades:
1ra.- La suma de los ángulos interiores de un polígono convexo de "n" lados es igual a tantas veces un ángulo llano como lados menos dos tiene el polígono.
2da.- El valor de un solo ángulo interior de un polígono convexo regular de "n" lados es:
3ra.- La suma de los ángulos exteriores de un polígono convexo es igual a 4 ángulos rectos:
4ta.- El valor de un solo ángulo exterior de un polígono regular convexo de "n" lados es:
5ta.- La suma de los ángulos centrales de un polígono convexo regular es igual a 4 ángulos rectos.
6ta.- El valor de un solo ángulo central de un polígono convexo regular de "n" lados es: 360º/n
7ma.- El número total de diagonales de un polígono es: De cada vértice de un polígono se pueden trazar (n - 3) diagonales; de los "n" vértices se podrán trazar n(n - 3) diagonales, pero todo sobre dos, pues cada diagonal corresponde a dos vértices diferentes.
12 ND= n(n-3) 2’>
8va.- La suma de los ángulos interiores de un polígono cóncavo es igual a tantas veces un ángulo llano como lados menos dos tiene el polígono.
Si= 180º(n-2)
9na.- La suma de los ángulos exteriores de un polígono cóncavo es igual a 4 ángulos rectos.
PROBLEMAS DE POLIGONOS
- ¿En qué polígono se cumple que el número de lados es igual al número de diagonales? Rpta.- Pentágono
- El doble del perímetro de un polígono equivale numéricamente a la cantidad total de diagonales que se puede trazar. Si cada lado del polígono mide 1,75cm ¿Cuántos lados tiene el polígono? Rpta.- 10
- ¿En qué polígono se cumple que el número de lados, más el número de ángulos internos, más el número de diagonales trazadas desde un vértice, es 15? Rpta.- hexágono
- ¿Cuántos lados tiene el polígono donde el número de lados excede en 2 al número de diagonales? Rpta.- 4
- En un polígono regular se cumple que la suma de medidas de los ángulos interiores es 6 veces la medida de un ángulo interior. ¿Cuántos lados tiene dicho polígono? Rpta.- 6
- ¿En qué polígono se cumple que el número de lados más la mitad del número de vértices es igual al número de diagonales? Rpta.- 6
- ¿Cuántos lados tiene el polígono convexo en el que la suma de los ángulos internos es 8 veces la suma de los ángulos externos? Rpta.- 18
- Cinco ángulos de un hexágono miden 120º, 130º, 140º, 150º y 160º. Halla la medida del sexto ángulo. Rpta.- 20º
- Calcula el número de diagonales de un polígono regular, sabiendo que la medida de cada ángulo externo equivale a un tercio de la medida de un ángulo interno. Rpta.- 20
10. ¿Cuántas diagonales tiene el polígono convexo cuya suma de sus ángulos interiores es 3600º? Rpta.- 209
11. ¿Cuántos lados tiene un polígono cuyo número de diagonales es el quíntuple del número de sus vértices? Rpta.- 13
12. ¿En qué polígono regular se cumple que la medida del ángulo exterior es el doble de la del ángulo interior? Rpta.- 3
13. ¿Cuántos lados tiene un polígono regular si la medida de su ángulo central es la mitad de la medida de su ángulo interior? Rpta.- 6
14. La diferencia de medidas de un ángulo interior y exterior de un polígono regular es 90º ¿Cuántos lados tiene dicho polígono?
15. Determina cuántos lados tiene un polígono convexo cuyo número de diagonales excede en 8 al número de diagonales de otro polígono que tiene un lado menos. Rpta.- 10
16. La suma de los ángulos interiores, exteriores y centrales de un polígono regular es 1260º. Calcula el número de lados del polígono. Rpta.- 5
17. Determina el número de diagonales de un polígono regular, sabiendo que la medida del ángulo interior es el doble de la medida de un ángulo central. Rpta.- 9
18. Si el número de vértices de un polígono regular aumenta en tres, el número de diagonales aumenta en 18. Calcula la medida del ángulo interior del polígono original. Rpta.- 120º
19. ¿Cuánto mide el ángulo central del polígono regular que tiene 170 diagonales? Rpta.- 18º
20. Si a un polígono regular se le disminuye cinco lados, el número de sus diagonales disminuye en 40. Calcula la medida del ángulo central del polígono original. Rpta.- 30º
21. Determina cuántos ángulos agudos puede tener como máximo un polígono convexo de n lados. Rpta.- n <>
Al aumentar en 2 el número de lados de un polígono regular la medida de su ángulo externo disminuye en 15º. ¿Cómo se llama el polígono regular? Rpta.- hexágono
22. Si el número de lados de un polígono aumenta en 3, el número total de diagonales se cuadruplica. Halla el polígono final. Rpta.- hexágono
23. En que polígonos al sumar el número de diagonales más el número de lados se obtiene 21. Rpta.- heptágono
24. Alrededor de una ciudad hay 20 torres y entre cada dos torres hay una línea de alta tensión. ¿Cuántas líneas hay? Rpta.- 20 líneas.
25. Si se prolongan los lados de un pentágono regular ¿Cuánto medirá el ángulo convexo de esta estrella de 5 puntas? Rpta.-36º
1 comentario
angel -